发布时间:Dec. 20, 2022, 11:52 a.m.编辑:李佳生阅读(1442)
一、为什么需要重采样
1、多速率系统: 现实中一个庞大复杂的工程系统常常为多速率系统,顾名思义就是在系统过程中使用多个采样速率。在某些情况下,运行于某个速率的系统的一部分需要一个原来以另外某个速率采样的信号(转换专业音频到消费者的CD音频就是一个例子)。在这种情况下,原始信号的速率必须根据需要增加或减少。或者针对特定的用途,也可能以比实际需要更高的速率对原来的数据进行了采样,因此需要降低采样率,然后得到的数据就可以大幅度降低对数据吞吐量的要求,从而降低存储器、处理器的要求,提高处理效率并降低功耗。
2、采样定理: 如果模拟信号x(t)包含的最大频率是Fmax且以Fs> 2Fmax的频率被采样,则信号才能被完美还原
3、混叠: 当信号存在> Fs/2的成分时则会干扰带宽内频率成分的准确采样,导致混叠,表现为以Fs/2中心对称的多余频率成分。
4、重采样最基本过程: 为了防止上面说的混叠,需要在重采样时,将最大带宽外的频率成分去除掉。因此一般的重采样过程为: 降采样先滤波再抽取、升采样先插值再滤波,各种重采样算法的不同基本集中在滤波抗混叠这一部分。
5、两种最常见的重采样方法:
sinc重采样: 一种比较理想的重采样方法,在截止频率位置滚降快,混叠少,缺点是计算开销大。
(多相)FIR重采样: 保证效果的同时,计算开销小,在截止频率位置滚降不如sinc,混叠想对多,但同时也保留了带宽内最大频率附近的频率成分,衰减较少。
二、sinc重采样基本原理
1、使用sinc函数进行信号采样与重建
在数字信号处理中,sinc函数定义为:
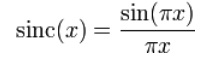
当x = 0时,sinc函数值为1,当x为整数时sinc函数值为0(这些整数点x称为过零点)。可以画出sinc函数的波形图如下:
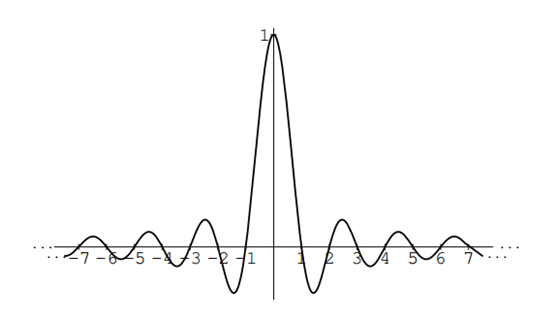
可以看出sinc函数是连续无限且关于Y轴对称的(即sinc函数是偶函数)。
采样定理说如果模拟信号x(t)包含的最大频率是Fmax且以Fs> 2Fmax的频率被采样,那么x(t)可以用插值函数:

从它的样本重建。这里的插值函数就是sinc函数。重建后的x(t)可表达为:
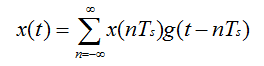
这里x(n/Fs) = x(nTs) = x(n)是x(t)的采样点值。Fs是采样频率,Ts是采样间隔,Fs = 1/Ts。
2、重采样
把数字信号的采样率从一个频率转换为一个另不同频率的过程称为重采样(sampling rate conversion,SRC)。上面采样定理说过如果信号的带宽小于采样率的一半,就可以用插值从样本重建信号。用新的采样率采样这个重建的信号,就可以实现重采样。
假设以Fx=1/Tx采样一个连续信号x(t),生成离散信号x(nTx)。使用插值公式:
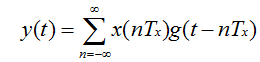
可以从样本x(nTx)生成连续信号y(t)。如果x(t)的带宽小于Fx/2且
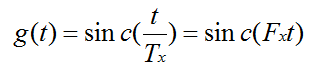
那么y(t) = x(t)。为了实现重采样,只需要以时间间隔t=mTy对y(t)进行求值即可,Fy=1/Ty是新的采样率。
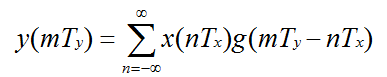
重新组织g(t)的参数:
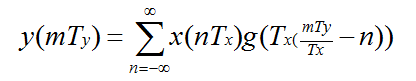
mTy/Tx可以分解成整数部分km和分数部分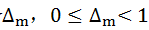
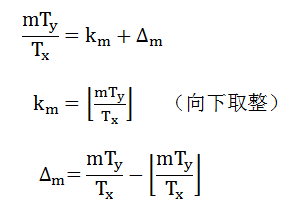
所以
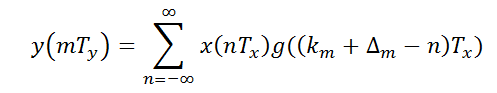
令k=km-n,所以 n =km – k, 从而
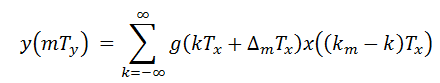
考虑到有上下采样,文档(https://ccrma.stanford.edu/~jos/resample/)给出插值函数为:
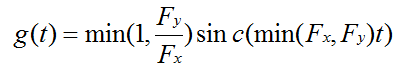
其中Fx为原采样率,Fy为新采样率。
令 A=min(1, Fy / Fx), B=min(Fx, Fy), ρ=Fy/Fx=Tx/Ty, 则g(t)可表示为
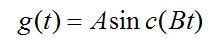
所以
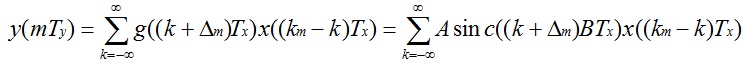
在上式中,x和y信号离散化后,在x信号和y信号中的Tx,Ty可以去掉了。式子就变成了如下:
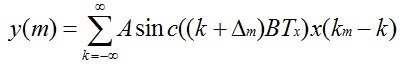
上式中BTx在Fx,Fy已知的情况下是个常数。
令D=BTx,上式就变成了:
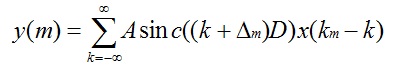
当上采样时B=Fx,则D=FxTx=1,A=1,所以式子重写为:
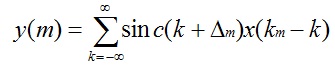
当下采样时B=Fy, 则D= FyTx = ρ A= ρ,所以式子重写为:
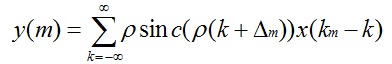
从上面的式子可以看出,新的采样率下的值是原采样率下的值和相对应的sinc函数的值的乘累加。由于sinc函数是连续且无限的,真正实现时是无法做到的,所以这儿通过截断sinc函数(比如使用Kaiser window加窗截断)并离散化,来获得近似信号。
三、多相FIR重采样基本原理
1、多相FIR滤波的基本原理
FIR的基本作用是充当低通滤波器,去掉多余的频率成分,减少混叠,相信大家都已经很熟悉FIR的工作原理与过程了,这里不多做介绍。
而多相FIR结构,则是一种可以极大减少计算量的方法,以2倍插值为例,Sin重采样至少可以等价于n阶FIR滤波计算,若用等价的多相FIR滤波器则可以减少2倍的计算量,下面介绍一下多相FIR的结构:多相插值滤波器将一组 N 阶FIR滤波器系数 ,映射为如下P个多相子滤波器结构,转换公式为: i∈[0, P-1]


下图为多相插值滤波器结构,该选项实现了计算效率高的1-to-P插值滤波器。

每个新的输入采样x(n)同时并行送入P个多相子滤波器,同时得到P个输出采样,每个多相子滤波器输出一个采样送到滤波器输出端口,输出端口从第一个多相子滤波器开始依次选择多相子滤波器的输出。由于输入采样是同时并行送入每个多相子滤波器的,因此多相插值滤波器的输出采样速率是输入数据采样速率的P倍。相对于较高的输出采样速率,多相子滤波器工作在比较低的频率上(对于输入采样速率),同样,在每个输出点上有N个操作。

2、利用对称性实现多相插值器
音频数据滤波时,我们总希望保持线性相位,这就需要FIR具有对称结构,并且对称结构可以使用一些代码来节约储存和计算开销。多相FIR可以利用如下对称性技术实现每组系数的对称处理。具体方法是通过在子滤波器系数的基础上加上和减去两个响应的非对称相位来得到包含对称系数的两个新相位,举例说明:
假设在一个阶数为15的滤波器,滤波器系数如下,对该滤波器进行3倍插值,得到3个子滤波器,系数分别为:

可见,第一个和第三个子滤波器是不对称的,应用对称性技术,经过简单的加法和减法运算对两个滤波器系数进行处理得到:

这样,h0为对称,而h2为负对称的。经过这样处理之后,实现这些子滤波器时就可以利用其对称性来节省资源。在输出端,第一个子滤波器的输出和第3个子滤波器的输出经过相加和相减运算后再乘以0.5就得到了原始滤波器的输出,如下图:

注:当用奇数个对称系数插值为2时,由于得到的多相子滤波器是对称的,所以不需要这种技术。
3、系数填充
在对称滤波器基础上进行插值,如果速率和滤波器阶数的组合导致子滤波器的系数个数不一致,则滤波器系数的重新组织将可能使滤波器的相位响应发生变化,即结果得到的冲激响应移位了若干个输出采样:
例如: 对阶数为14的滤波器进行4倍插值,则FIR需要有16阶才合理,这样的话,我们就需要在系数矢量的前面补充一个零,在系数矢量的后面也补充一个零系数,从而保证子滤波器系数的对称性,但结果是滤波器的相位响应发生了变化。
为了避免出现相位响应变化的方法是要么强制滤波器以非对称的结构实现,要么用能支持所选实现结构的额外系数来实现。下面给出了一些扩展到较大滤波器的例子:

更详细介绍可参考论文: ![]() Polyphase FIR Resample.pdf
Polyphase FIR Resample.pdf
上一篇:linux好用软件和常用指令